数理モデルを扱っていると、exp や log は日常的に登場します。
ブラック–ショールズ式でも、統計モデルでも、物理のボルツマン因子でも。
しかし、ふと立ち止まって考えたことはあるでしょうか。
なぜ exp の肩や log の中身は「無次元」でなければならないのでしょうか。
これは単なる形式的なルールではありません。
数式の「構造」に関わる本質的な話です。
log(5メートル)は意味を持つか?
例えば、
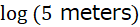
これは意味を持つでしょうか?
5メートルは「長さ」です。
しかし log は本来、
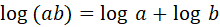
という性質を持ちます。
もし単位が入っていたら、
- meter の何乗?
- meter² はどう扱う?
- log(meter) って何?
という混乱が生じます。
log が定義できるのは、
「純粋な数」に対してのみです。
だからブラック–ショールズ式では、
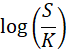
という「比」をとります。
価格 ÷ 価格。
単位が消え、無次元になります。
exp の肩が無次元でなければならない理由
指数関数はテイラー展開で定義されています。
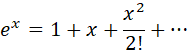
もし に単位があったらどうなるでしょうか?
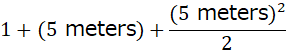
1 は無次元。
meter は長さ。
meter² は面積。
足し算ができません。
指数関数は「足し算」で構成されています。
だから肩は無次元でなければならないのです。
物理でも同じ
ボルツマン因子は
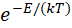
と書かれます。
ここでは
:エネルギー
:エネルギー
エネルギー ÷ エネルギー。
やはり無次元です。
物理では「次元解析」は基本中の基本です。
次元が崩れた瞬間、式は物理的意味を失います。
数理モデルにおける「守護神」
実務でもこれは強力なチェック機能になります。
あるとき、バリアオプションの解析式を制御変数として実装していた際、
モンテカルロと解析式が一致しませんでした。
計算自体は正しく見える。
しかしよく見ると、
log の中身が無次元になっていなかった。
そこがバグでした。
次元解析は、
数式の「健全性」を守る守護神です。
まとめ
- log の中身は無次元でなければならない
- exp の肩は無次元でなければならない
- これは単なる慣習ではなく、構造上の必然
数式の美しさは、
往々にして「次元が整っている」ことにあります。
そしてその整合性は、
理論だけでなく実務でも私たちを助けてくれます。
数式を扱うとき、
一度立ち止まって次元を確認してみてください。
意外なバグや誤解を、
静かに修復してくれるかもしれません。
コメントを残す